Алгоритмы прямой коррекции ошибок и особенности их применения. Турбо-код
 На данный момент развитие технологий прямой коррекции ошибок позволило современным телекоммуникационным системам достичь значительных результатов в приближении к верхней границе максимального количества передаваемых безошибочных цифровых данных (пределу Шеннона). Теоретически это понятие представляет собой максимальный уровень информационного контента для любого канала передачи. Нужно отметить, что использование технологии прямой коррекции ошибок не ведет к увеличению пропускной способности канала, наоборот, она даже несколько уменьшается из-за избыточных данных, так как ключевой особенностью технологии FEC является добавление дополнительных данных к передаваемому потоку, что позволяет принимающему устройству выявлять и исправлять ошибки, возникающие при передаче. Выигрыш в объеме информации, посылаемой по некоему каналу с помощью прямой коррекции ошибок (в отличие от каналов без нее), достигается исключительно благодаря тому, что данные гарантированно доходят до получателя. Другими словами, не нужны многократное дублирование, повторная отправка запроса на передачу и т. п., что с лихвой компенсирует их избыточность.
На данный момент развитие технологий прямой коррекции ошибок позволило современным телекоммуникационным системам достичь значительных результатов в приближении к верхней границе максимального количества передаваемых безошибочных цифровых данных (пределу Шеннона). Теоретически это понятие представляет собой максимальный уровень информационного контента для любого канала передачи. Нужно отметить, что использование технологии прямой коррекции ошибок не ведет к увеличению пропускной способности канала, наоборот, она даже несколько уменьшается из-за избыточных данных, так как ключевой особенностью технологии FEC является добавление дополнительных данных к передаваемому потоку, что позволяет принимающему устройству выявлять и исправлять ошибки, возникающие при передаче. Выигрыш в объеме информации, посылаемой по некоему каналу с помощью прямой коррекции ошибок (в отличие от каналов без нее), достигается исключительно благодаря тому, что данные гарантированно доходят до получателя. Другими словами, не нужны многократное дублирование, повторная отправка запроса на передачу и т. п., что с лихвой компенсирует их избыточность.
Вот почему микросхемы прямой коррекции ошибок успешно применяется для снижения затрат и увеличения производительности в различных беспроводных системах связи, таких как спутники, локальные беспроводные и оптоволоконные сети. Кроме того, разработаны высокоскоростные кремниевые интегральные схемы для FEC-приложений, перспективные для дальнейшего улучшения и оптимизации проектирования систем связи.
Поскольку технология активно развивается, а алгоритмы кодирования совершенствуются — количество ошибок, которые могут быть скорректированы при передаче, также увеличивается. Шумные каналы создают относительно больше ошибок, и возможность исправить их означает, что, даже при использовании такого канала передаваемые данные будут доставлены практически без потерь. Внедрение этой технологии ведет к таким системным усовершенствованиям, как увеличение эффективности полосы пропускания и скорости передачи данных, большей энергетической эффективности и, как следствие, к снижению экономических затрат на обеспечение стабильных каналов связи.
Как уже говорилось, технология FEC предполагает, что информация будет закодирована. Исходные данные пользователя, которые должны передаваться по каналу, называются битами информации, а данные, полученные после добавления информации коррекции ошибок, — кодированными битами.
Для битов информации k, результатом процесса кодирования является n кодированных битов, где n всегда больше k. После чего все n‑биты передаются получателю. На принимающей стороне выполняются измерения характеристик канала, и генерируется оценка переданных n‑битов. Декодер использует эти n‑биты оценки, наряду со знанием того, как были созданы все n‑биты для генерации оценок k‑битов информации. Процесс декодирования эффективно обнаруживает и исправляет ошибки в n‑битовых каналах оценок при восстановлении исходных k‑информационных битов.
Для генерации оценки n‑битов, в качестве промежуточного шага процесса коррекции ошибок, декодирования не требуется. В качественно спроектированном декодере квантованные данные канала измерения берутся с входа декодера. Эти исходные данные измерений канала состоят из n‑метрик, где каждая метрика соответствует вероятности того, что конкретный бит является логической единицей. Вероятность того, что заданный бит представляет собой логический ноль, также связана с данным числом. Эти показатели обычно представлены в виде 3‑ или 4‑разрядных целых чисел и называются метриками максимального правдоподобия. Выход декодера — это вычислитель k‑информационных битов. Как правило, декодирование метрик максимального правдоподобия является вычислительно интенсивным и очень часто выполняется на ASIC-декодерах, специально разработанных для выполнения указанной задачи.
Эффективность кода очень зависит от зашумленности канала передачи данных. Чтобы облегчить сравнение одного кода с другим, используется модель, когда шум добавляется к антиподальным сигналам. В этой модели шум является аддитивным белым гауссовым шумом (АБГШ). Несвязанные выборки шума добавлены к антиподальными символам канала (рис. 1). Дисперсия шума связана с мощностью спектральной плотности шума (No). Антиподальная сигнализация, показывает, где будут передаваться единицы и нули, посылаемые как +Z и –Z. В канале передачи Z может быть представлена в виде 1V. Так, единицы и нули будут передаваться как +1V и –1V соответственно. Полученная энергия на передаваемый бит данных (Еb) пропорциональна Z2. Важным параметром в системе представляется отношение уровня сигнала к шуму — отношение Eb/No. Модель (АБГШ) точно демонстрирует множество типов реальных каналов. Различные виды ошибок, многократно проявляющиеся в канале, также имеют АБГШ-подобный вид.
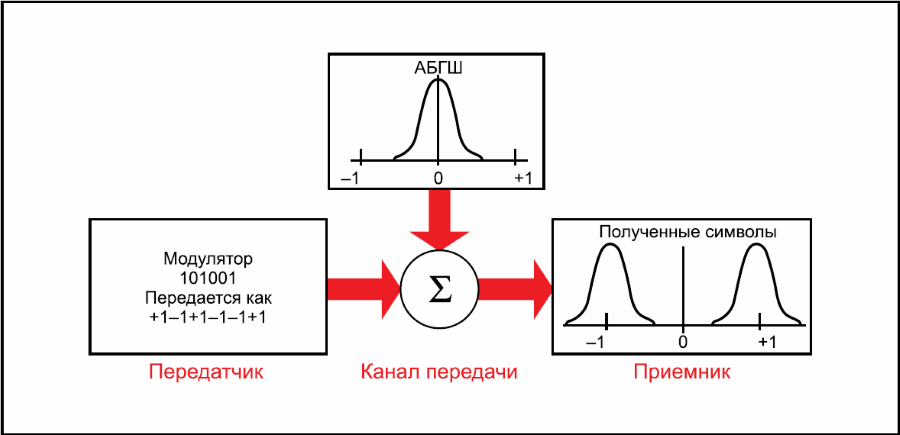
Рис. 1 - Добавление шума к исходному сигналу
FEC-коды бывают двух основных типов: сверточные и блочные. Рассмотреть их работу можно на примере абстрактных устройств, не вдаваясь в их схемотехнику. В простом сверточном кодере последовательность информационных битов проходит через регистр сдвига, и для каждого бита информации генерируются два выходных бита. Затем два выходных бита передаются. По существу, декодер оценивает состояние кодера для каждого набора из двух получаемых символов канала. Если декодер точно знает последовательность состояний кодера, он также знает исходную последовательность информации. Пример сверточного кода — разработанный В 1967 году Эндрю Витерби алгоритм декодирования, основанный на принципе максимального правдоподобия, позднее названный его именем.
Блочный код немного проще. Кодовый блок будет принимать K информационных битов и генерировать один или несколько битов четности. Эти биты четности добавляются к информационным битам, в результате чего образуется группа из N битов, где N > K. Закодированный модуль из N битов называется кодовым словом, и это кодовое слово передается целиком. На рис. 2 показан принцип работы (n, k) = (8, 4) кодового блока кодера. Приемник получает метрики канала n, а декодер оценивает наиболее вероятную последовательность (которых существуют 2000) согласно собранным данным. В блоках декодера, как правило, используется сложная алгебраическая структура, которая может быть применима для облегчения расшифровки. Пожалуй, наиболее популярным из ныне существующих блочных кодов является совместный код Рида — Соломона. Зачастую используют укороченный вариант, где n = 2040 кодов (255 байт). До недавнего времени самые мощные коды были построены из конкатенации сверточного кода и кода Рида — Соломона.
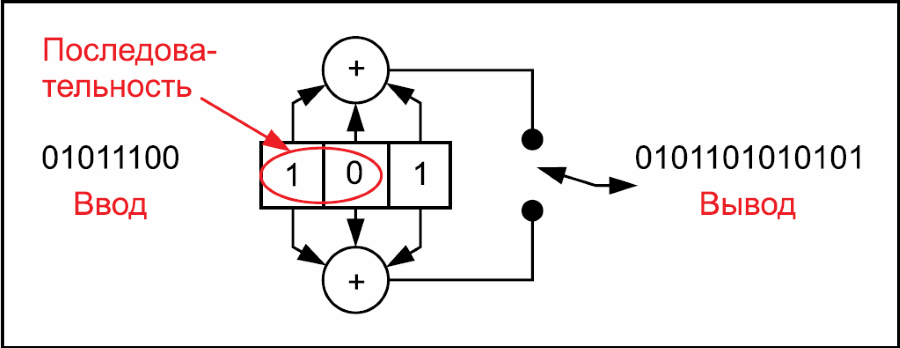
Рис. 2 - Принцип работы кодового блока кодера
Турбокод
Одним их последних значимых прорывов в развитии технологий FEC является класс кодов, называемых турбокодами. Это очень мощные коды, построенные из двух или большего числа кодов, меньших по размеру и более простых. Составные коды могут быть либо систематически-сверточными, либо блочными. Идея турбокодов состоит в том, чтобы единожды кодировать данные с помощью кодера 1, в некотором роде зашифровать порядок выходных битов, известных в приемнике, а затем кодировать эти биты вторым кодером. Передаются, соответственно, дважды закодированные биты. В приемнике процесс декодирования осуществляется в обратном порядке. Первое декодирование в соответствии с кодером 2, а второе декодирование в соответствии с кодером 1. Между двумя процессами декодирования операция скремблирования также происходит в обратном порядке.
Возможность провести процесс декодирования повторно делает турбокод уникальным. Второй составной декодер хранит в себе адреса ошибок, оставшиеся от первого. При повторном обращении к первому декодеру сохраняются адреса ошибок, оставшиеся от второго декодера. Скремблирование или чередование операций гарантирует, что ошибки, содержащиеся в одном из декодеров, будут видимы на другом декодере. Для того чтобы максимально увеличить эффективность, процесс декодирования обычно повторяется несколько раз. Причина в том, что ошибка может возникнуть не только в информационном бите, но и в любом из проверочных, а местоположение ошибки неизвестно. Каждая итерация приближает к правильному ответу, выдавая новые метрики правдоподобия и приближая декодер к исходному закодированному значению. Однако получение 100%-ной достоверности для каждого слова требует большого количества времени, поэтому итоговая производительность декодирования будет варьироваться в зависимости от количества итераций.
Для оптимальной работы итерационного процесса каждый составной декодер должен принимать метрики максимального правдоподобия (аналоговой обработки) и генерировать программируемый выходной сигнал, в соответствии с вероятностью нахождения каждого бита в закодированной последовательности. N‑выходные показатели учитывают избыточность кода, а также n‑программируемый входной сигнал. Декодер с использованием программируемого входного сигнала и генерации программируемого выходного сигнала уникален для турбокодов и значительно увеличивает сложность составных декодеров.
Принцип работы турбокода, где с выхода одного декодера подается входной сигнал на следующий декодер, в чем-то напоминает работу турбокомпрессора в двигателях внутреннего сгорания. Турбокомпрессор использует выхлопные газы двигателя (выход) для питания вентилятора турбины (вход), усиливая тем самым подачу воздуха. Таким образом объясняется наличие термина «турбо» в названии технологии турбокода. Турбокоды — это циклично декодируемые коды.
Технология турбокода наилучшим образом иллюстрируется на примере, где в качестве составных кодов используются блочные коды. Рассмотрим расширенный кода Хемминга (8,4), изображенный на схеме на рис. 3. Этот код использует четыре информационных бита, вычисляет 4 бит четности добавляет их к информационным битам для создания 8‑битного кодового слова для передачи: I1.1 I1.2 I1.3 I1.4 PH1.1 PH1.2 PH1.3 PH1.4 и т. д.
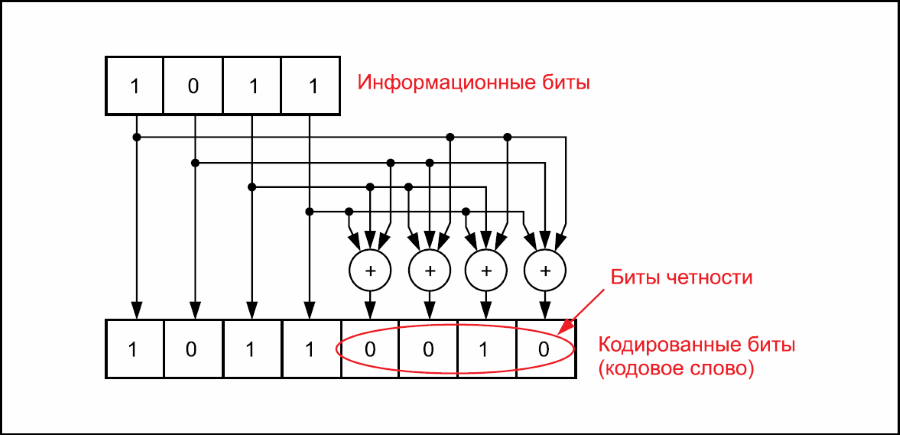
Рис. 3 - Схема расширенного кода Хемминга
Здесь I соответствует информационному биту и P соответствует битам четности или избыточности. Двумерный код продукта построенный из такого (8,4) расширенного кода Хэмминга может выглядеть следующим образом:

где I — информационный бит (числовой индекс показывает номер столбца и номер строки); PH — бит четности для каждого кодового слова, построенного по горизонтали (числовой индекс показывает номер строки и количество бит в слове); PV — бит четности для каждого кодового слова, построенного вертикально (числовой индекс показывает номер столбца и количество бит в слове); PVH — бит четности кодированных битов четности (числовой индекс показывает номер столбца и номер строки, использованных для вычисления полностью).
Результирующая матрица представляет собой турбокод. Построенный из линейных блочных кодов, турбокод обладает свойствами всех строк и всех столбцов, образующих кодовые слова. Различные коды могут использоваться для горизонтального и вертикального блоков, что позволяет обеспечить широкий спектр скоростей передачи кода и размеров блоков. Кроме того, возможны коды с 3D-структурой.
Единовременно выполняется декодирование одной результирующей матрицы. Сначала расшифровываются все горизонтальные блоки, а затем все вертикальные или наоборот. Процедура декодирования повторяется несколько раз, чтобы максимизировать эффективность декодера. С каждой итерацией, как уже было описано, декодер получает новые метрики правдоподобия, которые отражают, насколько близко удалось подойти к исходному значению передаваемых данных. На основании этих метрик может выполняться следующая итерация, корректирующая очередную битовую ошибку.
Рабочие характеристики турбокода лучше всего определяются с помощью компьютерного моделирования. Производительность турбокода (TPC), построенного из (64,57) кодов, используемого в обоих, X‑ и Y‑измерениях, показана на рис. 4. Этот код называется (64,57)2 TPC, или (4096, 3249) TPC. Также включен график коэффициента ошибок (BER) передаваемых данных без кодирования на канале с АБГШ (AWGN). Различие в показателях отношения сигнал/шум (Eb/No) между кривыми эффективности коэффициента ошибок (BER-симуляция) с кодированием на канале и без такового, при заданной величине коэффициента ошибок, называется коэффициентом эффективности кодирования.
Как правило, показатель, используемый для оценки качества обслуживания (QoS) канала связи, — это коэффициент ошибок (BER). Хотя этот показатель не всегда применим. Например, в сетях, где передаются пакеты данных, любое количество ошибочных битов в пакете составляют ошибку пакета. Когда это происходит, пакет данных отбрасывается и запрашивается повторная передача. В таком случае более подходящим показателем QoS-метрики является коэффициент пакетных ошибок. Когда при использовании прямой коррекции ошибок происходит одно событие ошибки, зачастую ошибочны несколько битов. Таким образом, эффективность коэффициента пакетных ошибок близка к эффективности коэффициента ошибок BER.
Если кодирование не применяется, пакетные ошибки возникают из случайных несвязанных входных битовых ошибок. Типичное событие пакетной ошибки имеет только один ошибочный бит во всем пакете. Как следствие, коэффициент пакетной ошибки значительно больше, чем коэффициент BER. Увидеть это можно на кривой коэффициента ошибок блоков кода (CER), показанной на рис. 4, на канале с некодированным сигналом. В данном примере размер пакета мы устанавливаем равным размеру кодового блока из 3249 бит.
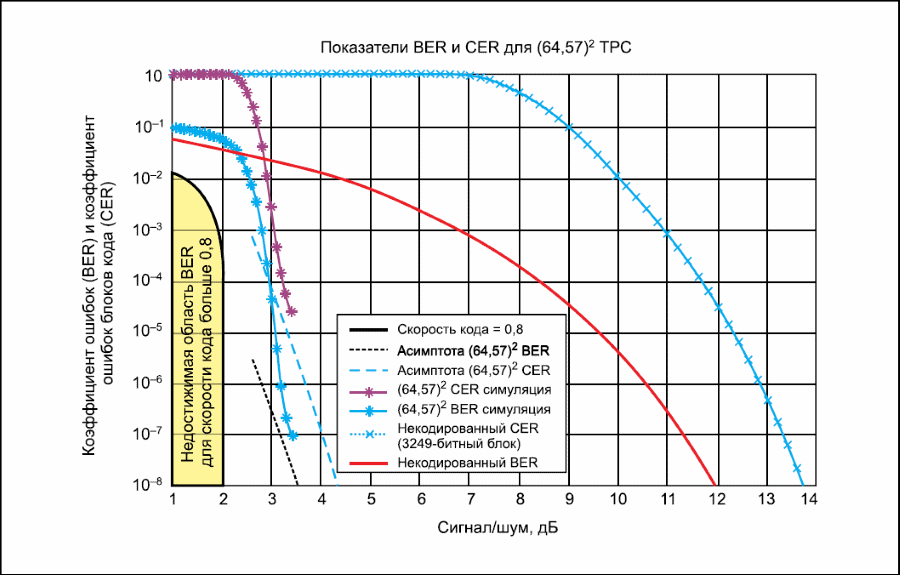
Рис. 4 - Производительность турбокода (ТРС)
Результаты моделирования (64,57)2TPC показывают исключительную производительность в пределах 1,2 дБ от теоретического предела Шеннона. Использование противоположной модуляции, BER = 10–6, и скорость кода = k/n = 0,8. Большие размеры блоков могут значительнее сократить этот разрыв.
Преимущества использования прямой коррекции ошибок
Прямая коррекция ошибок (FEC) независимо от других способов улучшения качества передачи данных повышает надежность их приема. Использование FEC в архитектуре системы позволяет разработчику системы прибегнуть к нескольким способам, обеспечивающим уверенный прием или передачу цифровых данных в различных условиях. Очевидное преимущество прямой коррекции ошибок — возможность ее использования в системах с ограниченной мощностью передатчика. Благодаря сигналам более высокого порядка также может быть решена проблема ограничения полосы пропускания, однако стоит заметить, что избыточность данных при применении FEC вносит ограничения в целесообразность употребления этого метода.
Во многих беспроводных системах допустимая мощность передатчика ограничена. Эти ограничения могут быть установлены для соблюдения требований стандарта или из практических соображений. Технология FEC делает доступной дополнительную пропускную способность канала, что дает возможность передавать информацию на более высоких скоростях.
Рассмотрим пример, где основным требованием является увеличение пропускной способности в системе с ограниченной мощностью. Предположим, что желаемое качество обслуживания сети (QoS-quality of service) достигается при коэффициенте ошибок BER = 10–6. Без кодирования приемнику требуется отношение сигнала к шуму, соответствующее Eb/No 10,5 дБ. Если используется турбокод (64,57)2ТРС, то QoS может поддерживаться при Eb/No 3,2 дБ. Таким образом, тот же энергетический сигнал может распространить в 5,3 раза больше битов информации. Кроме того, FEC обеспечит необходимые качество обслуживания сети (QoS). Однако для передачи в 5,3 раза больше данных понадобится в 5,3x(4096/3249), или в 6,68 раз, больше трафика. Если ширины полосы пропускания достаточно, пропускная способность может быть увеличена на коэффициент 5,3 без повышения мощности передатчика.
Большинство сетевых систем разработано для транспортировки пакетов данных. Когда канал приводит к возникновению одиночной битовой ошибки по всей длине пакета, он должен быть отброшен и повторно передан. Для таких систем показатель ошибки блока кода, также известный как коэффициент пакетной ошибки, используется для сравнения эффективности систем с применением FEC и без нее.
Для достижения показателя ошибки блока кода CER = 10–5 требуемое значение отношения Eb/No = 12,25 дБ для системы c незакодированным сигналом, в то время как система, использующая метод турбокода (64,57)2TPC, достигает аналогичного показателя ошибки CER при Eb/No = 3,4 дБ, что соответствует уменьшению нужной мощности в 8 раз. Это означает, что можно использовать маломощные усилители и меньшие антенны, в следствии чего стоимость такой системы существенно снизится.
Рассмотрим сценарий, в котором основным требованием является увеличение срока службы аккумулятора портативной беспроводной системы и, следовательно, уменьшение мощности передачи. Предположим, что желаемое качество обслуживания сети (QoS) достигается при показателе ошибок BER = 10–6. Использование турбокода (64,57)2TPC обеспечивает QoS на 3,2 дБ. Мощность передачи может быть урезана на коэффициент, равный 5,3. Для поддержания скорости передачи данных необходимо расширение полосы пропускания на 26% или (4096/3249). Если расширение невозможно, мощность передачи следует урезать на коэффициент, равный 6,8. Однако это приведет к снижению скорости передачи данных на 21% или (1–3249/4096). Если срок службы батареи не имеет значения, данные передаются на полной мощности. В этом случае коррекция ошибок FEC используется для передачи данных в большем диапазоне. Если снижение скорости передачи данных на 21% приемлемо, диапазон может быть расширенна 160%. Без мощной технологии коррекции ошибок FEC нужно будет применить либо усилитель высокой мощности, либо антенны большего размера. К сожалению, во многих системах такой подход невозможен, к тому же это увеличит стоимость самой системы.
Прямая коррекция ошибок успешно применяется и в оптоволоконных сетях. Вдоль всей протяженности трассы дальнемагистрального волокна предусмотрено некоторое количество оптических усилителей. Но это повышает стоимость, а также потребление электроэнергии системы. Интеграция FEC в подобную систему, в начале и в конце линии, может увеличить расстояние между этими узлами, что сведет к минимуму количество необходимых усилителей. Использование FEC либо увеличит ширину полосы пропускания, либо уменьшит пропускную способность. Высокоскоростные коды (k/n = скорость >0,75) сводят к минимуму этот эффект, не затрагивая высокую эффективность кодирования.
До сегодняшнего дня для решения данной задачи использовали либо некодированный сигнал, либо код Рида — Соломона, который был практически единственным доступным кодом, способным поддерживать необходи мые скорости для волокна (>1 Гбит/с). С появлением декодирующих TPC-микросхем предшествующий уровень развития технологии Рида — Соломона может быть улучшен почти на 4 дБ, что подразумевает значительное сокращение числа необходимых усилителей.
Если ограничение ширины полосы пропускания не является проблемой, для достижения более высокой пропускной способности при одновременном сохранении постоянной мощности передачи и полосы пропускания можно применить модуляции высшего порядка в сочетании с FEC.
Рассмотрим систему с некодирован ной структурой, реализованную на QPSK модуляциях с требуемым QoS при BER = 10–6. Нужный показатель отношения Eb/No = 10,5 дБ. Используя QPSK, которая составляет 2 бит на канал, показатель отношения Es/No (где Es — энергия на символ канала) составит 13,5 дБ.
Использование кодовой модуляции более высокого порядка, такой как Серокодированная 16‑QAM и ограничение канала в той же средней Es/No требуют такой же ширины полосы частот и мощность передатчика. Но уменьшенные интервалы между символами приводят к значительной деградации в QoS для BER = 10-2. Система реализации (64,57)2TPC может принимать QoS значительно ниже BER 10-15, будучи пригодной для всех практических целей, при полном отсутствии ошибок. Каждый переданный символ теперь носит 3,172 бит в среднем, что в 1,59 раза выше, чем в некодированной схеме QPSK.
Системы с кодовым разделением множественного доступа (Code division multiple access, CDMA) также получают большую пользу от FEC. Все пользователи, работающие в системе, могут рассматриваться как шум по отношению к любому произвольно выбранному пользователю. Применение FEC может значительно увеличить количество пользователей, одновременно работающих в системе. На самом деле максимальное число одновременно работающих пользователей в системе CDMA требует присутствия самого мощного из доступных кодов.
Проблема в том, что с использованием мощного FEC, шумность канала значительно возрастает и для получения выгоды от прямой коррекции ошибок аппаратная синхронизация носителя и время восстановления символа должны иметь значения, позволяющие работать в такой среде. Это может оказаться довольно сложной задачей, особенно если используется burst-модем, популярный в системах пакетной передачи данных.
Довольно старые коды Рида — Соломона — Витерби (RSV), по существу, блочные коды, могут генерировать довольно большие информационные блоки. Результатом станут значительное задержки, поскольку декодер не может генерировать выходные информационные биты, пока не будет получен весь блок. В системах RSV большие размеры блоков способны вызвать неприемлемые латентности. Турбокод может превосходить код RSV благодаря значительно более короткому размеру блока и, следовательно, уменьшать время задержки. Кроме того, чтобы достичь максимальной эффективности кодирования при низких скоростях битовых ошибок, размер блока Turbo Code обычно велик. Это приводит к увеличению задержки, хотя системы, работающие с низким уровнем битовых ошибок, как правило, являются системами с высшей скоростью передачи данных.
Исследования, направленные на поиск практически применимых кодов с еще большей эффективностью кодирования, ведутся непрерывно, но тот факт, что эффективность турбокода позволяет уже сейчас довольно сильно приблизиться к пределу Шеннона, означает, что дальнейшие усовершенствования будут постепенными и не столь значимыми.
Сверточные турбокоды (Turbo Convolutional Codes, или TCCs) выявляют вероятность ошибки и, таким образом, эффективны исключительно при более низких значениях битовых ошибок. Снижение или устранение вероятности ошибки является очень активной областью исследования, поскольку эта вероятность ограничивает использование сверточных тубокодов во многих системах.
TCCs и TPC имеют немного разные свойства, что делает их подходящими для различных областей применения.
Рассмотрев возможности турбокода, можно смело утверждать, что его массовое применение — вопрос времени. Поскольку все больше разработчиков систем связи знакомятся с возможностями дизайна систем, который становится доступным благодаря применению турбокода, распространяемого во все большем количестве систем. Третье поколение (3G) беспроводных сетей лишь один из примеров систем, где используется турбокод.
Новые системы связи уже сейчас разрабатываются с помощью различных вариантов турбокода FEC. Там, где требуется высокое качество обслуживания, низкие накладные расходы и высокие скорости передачи данных (многие спутниковые системы и сети с коммутацией пакетов), использование прямой коррекции ошибок становится идеальным выбором. А многие старые системы, в свою очередь, в настоящее время модернизированы для работы с турбокодом, и, несомненно, в дальнейшем его распространение будет расти, возможно, при исключении всех других типов прямой коррекции ошибок.
Данная статья была опубликована в журнале «Компоненты и технологии», № 11 '2016




