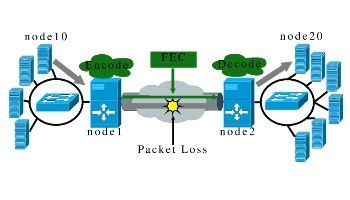
Прямая коррекция ошибок (FEC)
 Прямая коррекция ошибок (FEC) это метод, который использовался в течении нескольких лет в подводных оптоволоконных системах, проложенных по морскому дну. Этот метод позволяет с почти идеальной точностью передать данные, даже если передача осуществляется по каналу с большим количеством шумов. В настоящее время используется несколько алгоритмов FEC, таких как код Хэмминга, кода Рида-Соломона и код БЧХ.
Прямая коррекция ошибок (FEC) это метод, который использовался в течении нескольких лет в подводных оптоволоконных системах, проложенных по морскому дну. Этот метод позволяет с почти идеальной точностью передать данные, даже если передача осуществляется по каналу с большим количеством шумов. В настоящее время используется несколько алгоритмов FEC, таких как код Хэмминга, кода Рида-Соломона и код БЧХ.
В качестве примера, рассмотрим работу вашего мобильного телефона в условиях слабого сигнала сотовой сети. Допустим, вы хотели сказать человеку на другом конце линии некую последовательность чисел. Есть несколько методов, которые можно использовать для повышения точности. Предположим, что список чисел, которые вы хотите передать, это 7, 3, 8, 10, 12 и 21. Одним из способов может быть повтор списка чисел два раза. Запишите каждый список и сравните их, если они совпадают, передача данных, вероятно, корректна. Основным недостатком такого метода является то, что, поскольку данные передаются дважды, пропускная способность системы делится пополам и, если списки не совпадают, у вас не будет ни малейшего представления, который из них верный. Используя этот метод, для того, чтобы убедиться в хорошем качестве передачи и исправить некоторые ошибки, вам придется отправить данные три раза и проверить, что два из трех списков полностью совпадают. Второй способ будет выглядеть примерно так: в первую очередь, вы будете отправлять количество чисел, которые необходимо принять, затем саму последовательно, и в конце последует передача числа, являющегося суммой последовательности. Передаваемое сообщение при этом примет следующий вид: 6, 7, 3, 8, 10, 12, 21, и 67. Человек, принимающий сообщение, будет смотреть на первое число, чтобы затем убедится, что будет получено правильное количество чисел в сообщении, а затем проверит, что число в конце последовательности, действительно является суммой переданных чисел. Этот метод требует отправки значительно меньшего количества дополнительных данных. Если любое полученное число неверно или пропущено, то число контрольной суммы в конце передачи не будет соответствовать сумме, передаваемых чисел. Показанные выше методы представляют собой примеры кода обнаружения ошибок. Они позволяют определить, была ли передача точной, но не позволяют исправлять ошибки.
Примечание: Термин "Forward" в аббревиатуре FEC означает, что исправление ошибок осуществляется путем передачи некоторой информации вместе с передачей данных.
Код исправления ошибок считаются более сложными, в сравнении с кодом обнаружения ошибок и используются почти в каждом современном коммуникационном приложении. Также, коды исправления ошибок нашли широкое применение в CD и DVD проигрывателях. Для того, чтобы привести пример кода исправления ошибок, нужно ввести и объяснить два термина: двоичность и чётность. В предыдущих примерах кода обнаружения ошибок, мы использовали такие числа, как 7, 3, 8, и т.д. Это базовые числа системы исчисления, знакомой нам в повседневной жизни. Двоичные числа в основе имеют два числа, которые могут иметь только два возможных значения – 0 или 1. Бинарная система используется почти во всех коммуникационных и компьютерных системах. Второе определение, которое необходимо разобрать, называется четность. Чётность - термин, который используется в двоичных системах связи, чтобы указать, является ли число единиц в передаче четным или же нет. Если число единиц является четным, то чётность совпадает и наоборот.
Код Хэмминга
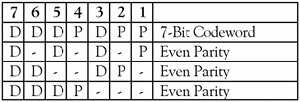
Рассмотрим сообщение, имеющее четыре бита данных (D), которое должно быть передано в 7-битной кодировке с добавлением трёх битов данных для поиска и устранения ошибок. Этот код будет называться (7, 4). Это означает, что общая длина кода составляет семь битов, но только четыре из них на самом деле данные. Три добавленных бита - это три бита проверки на четность (Р), где чётность каждого вычисляется в разных группах битов сообщения, как показано на рисунке 1.
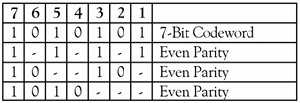
Например, сообщение 1011 будут направлено, как 1010101, как показано на рисунке 2.
Можно заметить, что в случае возникновения ошибки в любом из семи битов, эта ошибка оказывает влияние на различные комбинации трех битов четности в зависимости от битовой позиции.
Например, предположим, что вышеупомянутое сообщение 1010101 передаётся и возникает один бит ошибки, так что получено кодовое слово 1110101:
Передача Приём
Сообщение Сообщение
1 0 1 0 1 0 1 -----------> 1 1 1 0 1 0 1
Эта ошибка может быть исправлена путем определения, какой из трех битов четности пострадал, как показано на рисунке ниже:
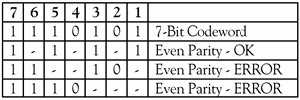
Характер ошибок четности битов указывает, какой бит в кодовом слове с ошибкой, таким образом, он может быть исправлен.
Основные функции кода Хэмминга можно резюмировать:
- Обнаружение 2-битовых ошибок (при условии отсутствия ошибок корректировка не выполняется)
- Коррекция единичных ошибочных битов
- 3 проверочных бита добавляется к 4-битовому сообщению
Способность корректировать одиночные ошибочные биты приводит к снижению себестоимости передачи, которая получается меньше, чем в случае отправки сообщения дважды целиком. (Напомним, что, просто отправив сообщение дважды коррекция ошибок не выполняется.) К тому же, при увеличении размера кодового слова, дополнительная нагрузка исправления ошибочных битов уменьшается. Например, одним из возможных вариантов кода Хэмминга для передачи по морским подводным оптоволоконным системам является код (18880, 18865). Это означает, что кодовое слово 18880 в действительности содержит 18,865 бит данных и 15 бит коррекции ошибок. Более надежные методы прямой коррекции ошибок (FEC) могут содержать гораздо больше битов коррекции ошибок, так что несколько ошибочных битов могут быть обнаружены и исправлены в каждом кодовом слове.
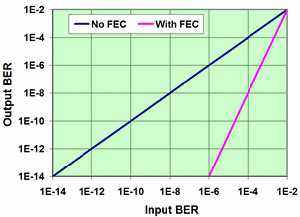 Существует метод прямой коррекции ошибок (FEC), аналогичный коду Хемминга. Как правило, в системах с оптической несущей ОС-192, накладывается около 7% дополнительной нагрузки на систему за счёт процесса коррекции ошибок (FEC). Допустим, базовая скорость передачи данных 10 Гбит/с, с учётом дополнительной нагрузки будет увеличена до 10,7 Гбит/с. Таким образом, с каждой 1000 бит передаваемых данных, отправляется ещё 70 бит коррекции ошибок, чтобы позволить провести проверку целостности полученных данных и исправить ошибки, которые могут возникнуть при передаче по оптическому каналу связи. На рисунке 4 показано влияние прямой коррекции (FEC) на системный коэффициент ошибочных битов (BER). Этот коэффициент является показателем числа ошибок в битах, деленное на общее число переданных битов в исследуемом временном интервале. BER 10-3 означает, что один из каждых 1000 бит будет передан некорректно. Синий график наглядно отображает количество передаваемых данных, если система не имеет FEC. Входной коэффициент BER (input BER) – это показатель ошибок, возникающих в канале передачи. Пока в системе отсутствует FEC, любые ошибки, которые происходят во время передачи появляются на выходе системы. Фиолетовый график показывает, что может произойти, если в системе используется FEC. В отсутствии FEC в системе входной коэффициент BER 10-6 даст аналогичное значение выходного BER 10-6, а в случае использования данной технологии происходит значительное улучшение выходной величины BER 10-14 (output BER).
Существует метод прямой коррекции ошибок (FEC), аналогичный коду Хемминга. Как правило, в системах с оптической несущей ОС-192, накладывается около 7% дополнительной нагрузки на систему за счёт процесса коррекции ошибок (FEC). Допустим, базовая скорость передачи данных 10 Гбит/с, с учётом дополнительной нагрузки будет увеличена до 10,7 Гбит/с. Таким образом, с каждой 1000 бит передаваемых данных, отправляется ещё 70 бит коррекции ошибок, чтобы позволить провести проверку целостности полученных данных и исправить ошибки, которые могут возникнуть при передаче по оптическому каналу связи. На рисунке 4 показано влияние прямой коррекции (FEC) на системный коэффициент ошибочных битов (BER). Этот коэффициент является показателем числа ошибок в битах, деленное на общее число переданных битов в исследуемом временном интервале. BER 10-3 означает, что один из каждых 1000 бит будет передан некорректно. Синий график наглядно отображает количество передаваемых данных, если система не имеет FEC. Входной коэффициент BER (input BER) – это показатель ошибок, возникающих в канале передачи. Пока в системе отсутствует FEC, любые ошибки, которые происходят во время передачи появляются на выходе системы. Фиолетовый график показывает, что может произойти, если в системе используется FEC. В отсутствии FEC в системе входной коэффициент BER 10-6 даст аналогичное значение выходного BER 10-6, а в случае использования данной технологии происходит значительное улучшение выходной величины BER 10-14 (output BER).
Таким образом, интеграция прямой коррекции ошибок в систему позволяет разработчику увеличивать расстояние и скорости передачи данных значительнее, чем при использовании любой другой технологии, а также увеличит срок службы системы.